Bentuk Umum Persamaan Kuadrat Adalah ax²
Hai, Sobat Matematika! Pernah merasa pusing tujuh keliling , ngeliatin soal-soal persamaan kuadrat? Rasanya kayak lagi menghadapi monster berkepala tiga ! Tenang aja, gak perlu panik !. Kali ini, kita bakal bahas bareng-bareng , bentuk umum persamaan kuadrat , yang ternyata gak serumit yang dibayangkan !. Siap-siap , otakmu bakal terbuka lebar , setelah baca artikel ini !.
Yap, kita akan menyelami dunia persamaan kuadrat , dengan membahas bentuk umumnya , yaitu ax² + bx + c = 0. Kelihatannya serem ya ? . Padahal , kalau udah paham , persamaan ini justru jadi sahabat terbaikmu , dalam memecahkan berbagai macam masalah , mulai dari menghitung luas lahan , sampai merancang jembatan !.
Kenapa ax² + bx + c = 0 dibilang bentuk umum? Karena , semua persamaan kuadrat , bisa ditulis dalam bentuk ini !. 'a', 'b', dan 'c' itu adalah konstanta , alias angka-angka , yang bisa bernilai positif , negatif , atau bahkan nol !. Yang penting , 'a' itu nggak boleh nol , lho !. Kalo 'a'-nya nol , persamaan itu udah bukan persamaan kuadrat lagi , melainkan persamaan linear !.
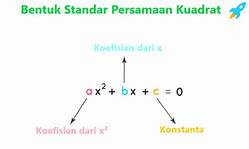
Nah , sekarang kita bedah satu-satu , arti dari setiap huruf !. 'a' ini adalah koefisien dari x² , alias angka yang nempel di depan x². 'b' adalah koefisien dari x , dan 'c' adalah konstanta , alias angka yang berdiri sendiri , tanpa x!. Contohnya , 2x² + 5x + 3 = 0. Di sini , a = 2 , b = 5 , & c = 3 !. Mudah , kan ? .
Dengan memahami bentuk umum ini , kita bisa dengan mudah mengidentifikasi , suatu persamaan , apakah termasuk persamaan kuadrat atau bukan !. Dan yang lebih penting lagi , memahami bentuk umum ini adalah kunci , untuk bisa menyelesaikan , berbagai jenis soal persamaan kuadrat , baik itu dengan cara memfaktorkan , melengkapi kuadrat sempurna , atau bahkan menggunakan rumus kuadrat !.
Jadi , jangan takut lagi dengan persamaan kuadrat!. Bentuk umum ax² + bx + c = 0 ini adalah jalan pintas , untuk menaklukkan monster matematika ini !. Simak terus artikel ini ya , karena kita bakal bahas lebih dalam lagi , tentang bagaimana menyelesaikan persamaan kuadrat , dengan berbagai metode !. Siap ? . Let’s go !.
Bentuk Umum Persamaan Kuadrat Adalah ax²: Panduan Lengkap
Pendahuluan: Mengenal Persamaan Kuadrat dan Pentingnya Memahaminya
Halo, Sobat Matematika! Pernahkah kamu mendengar istilah Persamaan Kuadrat? Mungkin terdengar asing, tapi sebenarnya persamaan ini sangat penting dan sering kita jumpai, baik disadari maupun tidak, dalam kehidupan sehari-hari. Memahami Persamaan Kuadrat akan membuka pintu pemahaman terhadap berbagai fenomena dan permasalahan, dari perhitungan sederhana hingga masalah kompleks dalam bidang sains dan teknik. Artikel ini akan menjadi panduan lengkap untuk memahami seluk beluk persamaan kuadrat, dari bentuk umumnya hingga aplikasinya dalam kehidupan nyata. Siap menjelajahi dunia Persamaan Kuadrat?
Heading 1: Mengenal Lebih Dekat Persamaan Kuadrat
Heading 2: Apa itu Persamaan Kuadrat?
Definisi sederhana Persamaan Kuadrat adalah suatu persamaan matematika yang pangkat tertinggi variabelnya (biasanya x) adalah dua. Bentuknya selalu melibatkan suku x², sehingga sering disebut juga sebagai persamaan tingkat dua. Karakteristik utama yang membedakannya dengan persamaan linear (pangkat satu) adalah keberadaan suku kuadrat ini.
Contoh persamaan kuadrat mudah ditemukan. Misalnya, perhitungan luas persegi dengan sisi x diwakili oleh persamaan Luas = x². Atau, lintasan proyektil yang membentuk parabola juga dapat dimodelkan menggunakan persamaan kuadrat.
Heading 2: Bentuk Umum Persamaan Kuadrat: ax² + bx + c = 0
Bentuk umum Persamaan Kuadrat ditulis sebagai ax² + bx + c = 0, di mana:
- a: Koefisien dari x², dan a ≠ 0. Jika a = 0, persamaan tersebut bukan lagi persamaan kuadrat, melainkan persamaan linear.
- b: Koefisien dari x.
- c: Konstanta (suku tetap).
Contoh:
- 2x² + 5x + 3 = 0 (a=2, b=5, c=3)
- x² - 4 = 0 (a=1, b=0, c=-4)
- -3x² + 2x - 1 = 0 (a=-3, b=2, c=-1)
Heading 2: Koefisien dan Konstanta dalam Persamaan Kuadrat
Koefisien a, b, dan konstanta c memiliki peran penting. Nilai a menentukan apakah parabola terbuka ke atas (a > 0) atau ke bawah (a < 0). Nilai b dan c memengaruhi posisi parabola pada sumbu koordinat, menentukan titik puncak dan titik potong dengan sumbu x dan y.
Heading 1: Memecahkan Persamaan Kuadrat
Ada beberapa metode untuk menyelesaikan Persamaan Kuadrat, yaitu:
Heading 2: Metode Pemfaktoran
Metode ini melibatkan pemfaktoran persamaan kuadrat menjadi dua faktor linear. Metode ini efektif jika persamaan mudah difaktorkan. Jika tidak, metode ini kurang efisien.
Contoh: x² + 5x + 6 = 0 dapat difaktorkan menjadi (x+2)(x+3) = 0, sehingga x = -2 atau x = -3.
Heading 2: Metode Kuadrat Sempurna
Metode ini mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna, lalu dicari akarnya. Metode ini berguna jika pemfaktoran sulit dilakukan.
Heading 2: Rumus ABC (Rumus Kuadratik)
Rumus ABC, x = [-b ± √(b² - 4ac)] / 2a, adalah metode umum untuk menyelesaikan persamaan kuadrat. Diskriminan (D = b² - 4ac) menentukan jenis akarnya: D > 0 (dua akar real berbeda), D = 0 (dua akar real kembar), D < 0 (dua akar imajiner).
Heading 2: Grafik Persamaan Kuadrat (Parabola)
Grafik persamaan kuadrat berbentuk parabola. Titik puncak (Vertex) parabola dapat ditentukan dengan rumus x = -b/2a, lalu substitusikan ke persamaan untuk mencari nilai y. Titik potong sumbu x didapat dengan menyelesaikan persamaan kuadrat, sementara titik potong sumbu y didapat dengan mensubstitusikan x = 0 ke persamaan.
Heading 1: Aplikasi Persamaan Kuadrat dalam Kehidupan Sehari-hari
Heading 2: Persamaan Kuadrat dalam Fisika
Persamaan Kuadrat digunakan dalam perhitungan lintasan peluru, ayunan bandul, dan berbagai fenomena fisika lainnya.
Heading 2: Persamaan Kuadrat dalam Ekonomi
Analisis fungsi permintaan dan penawaran seringkali melibatkan persamaan kuadrat.
Heading 2: Persamaan Kuadrat dalam Teknik Sipil
Perhitungan struktur bangunan dan jembatan seringkali menggunakan konsep Persamaan Kuadrat.
Kesimpulan: Menguasai Persamaan Kuadrat untuk Kehidupan yang Lebih Baik!
Memahami Persamaan Kuadrat membuka peluang untuk memecahkan berbagai masalah dalam berbagai bidang. Praktikkan terus pemahamanmu, dan jangan ragu untuk mencari sumber belajar tambahan!
FAQ (Pertanyaan yang Sering Diajukan)
- Apa bedanya persamaan kuadrat dengan persamaan linear? Persamaan linear pangkat tertinggi variabelnya 1, sedangkan persamaan kuadrat pangkat tertinggi variabelnya 2.
- Bagaimana cara menentukan jenis akar persamaan kuadrat? Dengan menghitung diskriminan (D = b² - 4ac).
- Apa aplikasi persamaan kuadrat di bidang lain selain yang telah disebutkan? Banyak! Di bidang komputer grafik, desain, dan masih banyak lagi.